Paragraph rule state machine

bool BlockRules::RuleParagraph(StateBlock& state, int start_line, int end_line,
                               bool silent) {
  // If this is an empty line -> not a paragraph
  if (state.IsEmpty(start_line)) return false;

  std::vector<std::pair<std::string, RuleBlock>> terminator_rules =
      state.md.block_parser.ruler.GetRules("paragraph");

  ParentType old_parent_type = state.parent_type;
  state.parent_type = ParentType::kParagraph;

  int next_line = start_line + 1;

  // Move line-by-line until we find a terminator
  for (; next_line < end_line && !state.IsEmpty(next_line); next_line++) {
    // Code-indented line after a paragraph = lazy continuation
    if (state.s_count[next_line] - state.blk_indent > 3) continue;

    // Blockquote marker quirk (negative indent)
    if (state.s_count[next_line] < 0) continue;

    // Run terminator rules
    bool terminate = false;
    for (std::pair<std::string, RuleBlock>& rule : terminator_rules) {
      if (rule.second(state, next_line, end_line, true)) {
        terminate = true;
        break;
      }
    }
    if (terminate) break;
  }

  // Extract raw paragraph text
  std::string content =
      state.GetLines(start_line, next_line, state.blk_indent, false);
  content = Utils::Trim(content);

  state.line = next_line;

  // Build tokens
  Token& token_open = state.Push("paragraph_open", "p", Nesting::kOpening);
  token_open.map =
      std::optional<std::pair<float, float>>({start_line, state.line});

  Token& token_inline = state.Push("inline", "", Nesting::kSelfClosing);
  token_inline.content = content;
  token_inline.map =
      std::optional<std::pair<float, float>>({start_line, state.line});

  state.Push("paragraph_close", "p", Nesting::kClosing);

  state.parent_type = old_parent_type;

  return true;
}

1. Input Alphabet

Let the input lines be:

\Sigma = \{ L_0, L_1, \dots, L_{n-1} \}

Each line

L_i

is a tuple:

L_i = (text_i, empty_i, s\_count_i)

where:

$empty_i \in \{0,1\}$ indicates if the line is empty
$s\_count_i$ is the leading space count
$text_i$ is the raw text of the line

Let

blk\_indent

be the block indentation of the paragraph, and

end\_line

be the specified or actual last line, and

\mathcal{T}

the set of terminator rules:

\mathcal{T} = \{ \tau_j : (state, i) \mapsto \{0,1\} \}

Each

\tau_j

is a predicate corresponding to a block-level terminator.

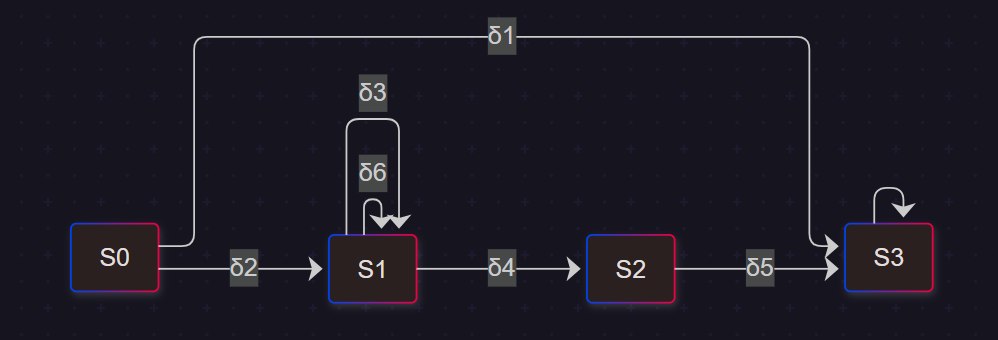
2. State Machine Definition

We model RuleParagraph as a deterministic state machine:

M_{paragraph} = (Q, \Sigma, \delta, q_0, F)

States

Q = \{ S_0, S_1, S_2, S_3 \}

$S_0$ : initial line evaluation
$S_1$ : scanning subsequent lines until termination
$S_2$ : extract paragraph content and build tokens
$S_3$ : final state

Initial State

q_0 = S_0

Final State

F = \{ S_3 \}

State Variables

$i$ : current line index
$next\_line$ : scanning index
$parent\_type$ : current block context
$terminate \in \{0,1\}$ : flag indicating terminator hit

3. Transition Rules

3.1 Start State ( $S_0$ )

S_0

, reject if the line is empty: If:

empty_{start\_line} = 1

Then:

\delta_1: \delta(S_0, start\_line) = (S_3)

Otherwise:

\delta_2: \delta(S_0, start\_line) = (S_1, start\_line + 1)

3.2 Scan State ( $S_1$ )

For

i = next\_line

, continue scanning while all conditions hold:

\begin{aligned} i &< end\_line &\land \\ empty_i &= 0 &\land \\ s\_count_i - blk\_indent &\le 3 &\land \\ s\_count_i &\ge 0 &\land \\ \forall \tau_j \in \mathcal{T},\ \tau_j(state,i) &= 0 \end{aligned}

Then:

\delta_3: \delta(S_1, i) = (S_1, i+1)

\delta_6:\ \delta(S_1, i) = (S_1, i+1) \quad\text{iff } s\_count_i < 0

Otherwise if :

\begin{aligned} i &\ge end\_line &\vee \\ empty_i &= 1 &\vee \\ s\_count_i - blk\_indent &> 3 &\vee \\ s\_count_i &< 0 &\vee \\ \exists \tau_j \in \mathcal{T},\ \tau_j(state,i) &= 1 \end{aligned}

\delta_4: \delta(S_1, i) = (S_2, i )

3.3 Extract State ( $S_2$ )

S_2

, the machine:

$S_2$ the paragraph content:

content = Trim(state.GetLines(start_line, i, blk_indent))

Builds the tokens:

Open token: paragraph_open
Inline token: inline with content
Close token: paragraph_close

Then transition to final state:

\delta_5: \delta(S_2, i) = (S_3, i)

4. Tabular Format

Current State	Input / Condition	Next State	Output / Action	Transition
$S_0$ (Start)	$empty_{start\_line} = 1$	$S_3$ (Done)	None	$\delta_1$
$S_0$ (Start)	$empty_{start\_line} = 0$	$S_1$ (Scan)	Init `next\_line = start\_line + 1`; load $\mathcal{T}$ ; set `parent_type = Paragraph`	$\delta_2$
$S_1$ (Scan)	$i \ge end\_line$	$S_2$ (Extract)	End-of-block reached	$\delta_4$
$S_1$ (Scan)	$empty_i = 1$	$S_2$ (Extract)	Empty line terminates paragraph	$\delta_4$
$S_1$ (Scan)	$s\_{count_i} - blk\_indent > 3$	$S_2$ (Extract)	Indent too deep → terminate paragraph	$\delta_4$
$S_1$ (Scan)	$s\_{count_i} < 0$	$S_1$ (Scan)	Blockquote quirk → skip line	$\delta_6$
$S_1$ (Scan)	$\exists \tau_j\in\mathcal{T}:\tau_j(state,i)=1$	$S_2$ (Extract)	Terminator rule fires	$\delta_4$
$S_1$ (Scan)	$(i < end\_line)\land(empty_i=0)\land(s\_{count_i}-blk\_indent \le 3)\land(s\_{count_i}\ge 0)\land(\forall j:\tau_j=0)$	$S_1$ (Scan)	Normal continuation: advance to $i+1$	$\delta_3$
$S_2$ (Extract)	—	$S_3$ (Done)	Extract text, trim, generate tokens	$\delta_5$
$S_3$ (Done)	—	—	Restore `parent_type`, assign `state.line`, return `true`	—

5. Image

Overview

Getting Started

Guides

State Machines & Internals

Performance

Paragraph rule state machine

1. Input Alphabet

2. State Machine Definition

States

Initial State

Final State

State Variables

3. Transition Rules

3.1 Start State ( $S_0$ )

3.2 Scan State ( $S_1$ )

3.3 Extract State ( $S_2$ )

4. Tabular Format

5. Image

Overview

Getting Started

Guides

State Machines & Internals

Performance

​1. Input Alphabet

​2. State Machine Definition

​States

​Initial State

​Final State

​State Variables

​3. Transition Rules

​3.1 Start State (S0S_0S0​)

​3.2 Scan State (S1S_1S1​)

​3.3 Extract State (S2S_2S2​)

​4. Tabular Format

​5. Image

1. Input Alphabet

2. State Machine Definition

States

Initial State

Final State

State Variables

3. Transition Rules

3.1 Start State ( $S_0$ )

3.2 Scan State ( $S_1$ )

3.3 Extract State ( $S_2$ )

4. Tabular Format

5. Image